LASSO method for Conditional Autoregressions and Experimental design

Background

Species formed complex networks. It is often time hard to direct measure the network and interactions between species. It is especially true that for taxa of microbe that cannot be cultured (alone) in the lab.

We might be able to heat the environment, applying some anti-biotics, and other sorts of indirect manipulations. We can observe the abundance/composition/presence of species under such manipulation. From there, how can we decode the interactions?

Take a close look to the question, it can be understand as a graphical selection problem, i.e. there exist two sets of nodes, the environment (predictors) and the species (nodes) and some edges encode the conditional (in)dependence. There are directed edges from environments to species and some undirected edges between species. Let’s assume the graph is sparse, which is common in a lot of practice. The question reduce to how we might find such a graph?

The model

Alright, we can further simplify the problem to Normal case, which is tractable and can act as a “core” for other type of responses. The model that account for conditional dependence between environment and species? Conditional Auto-Regression (CAR) model is a natural choice. Our goal was to study the sparse regression of such model. We took a Bayesian approach, view the LASSO penalty as LASSO prior, then we can derive a Gibbs sampler to sample from the posterior efficiently…

Some results

Speed

The model (CAR-LASSO) is quite fast, we did experiment with a i7 desktop with windows 7 OS:

Accurancy

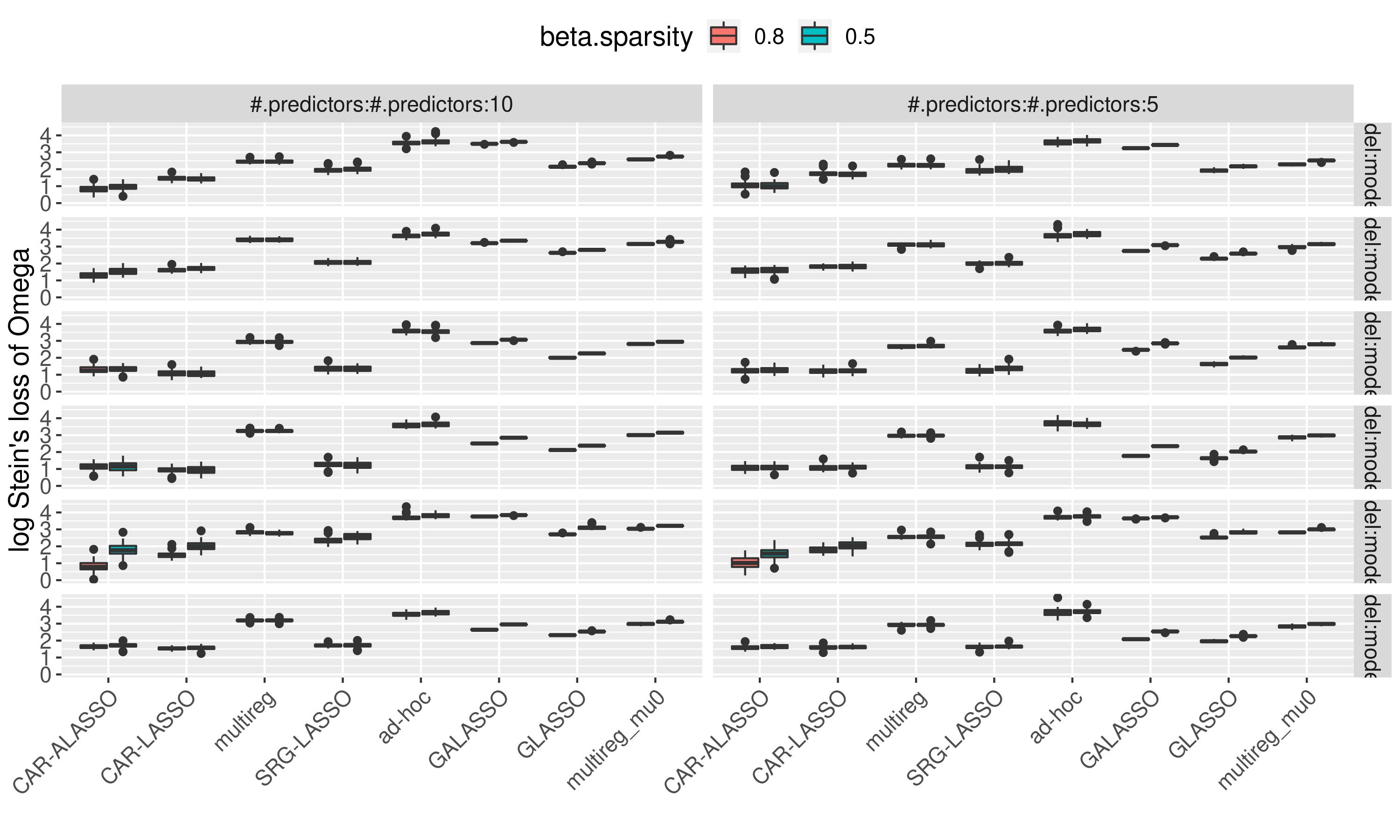
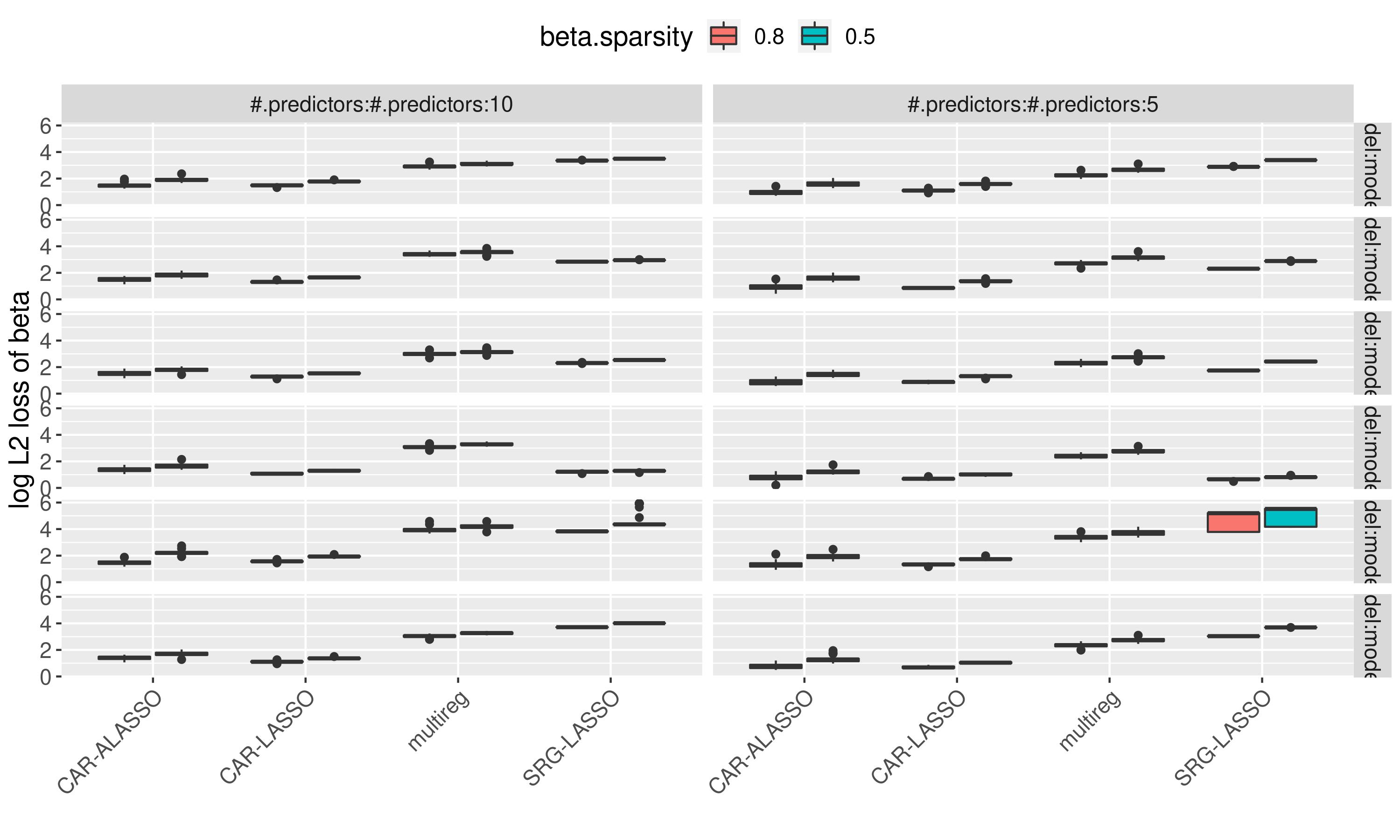
We compared it with several other models for a 30-nodes 10 or 5 predictors system on 6 different graph structure..

Stein’s Loss of the graph within nodes

log L2 Loss of the edges between predictors and nodes

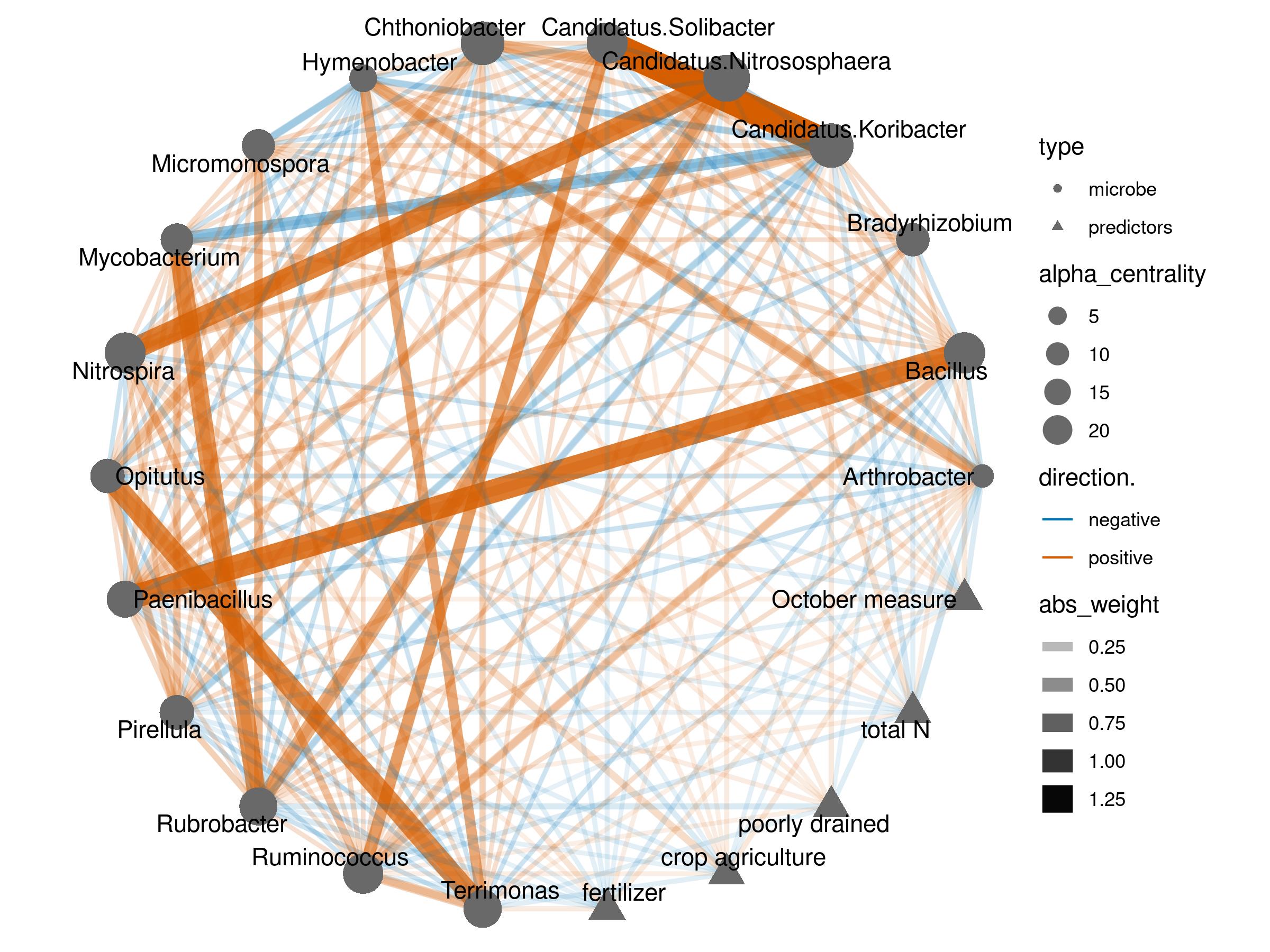
Real data example

We applied the model to two real world datasets. One from human gut, the other from soil. We mapped the conditional auto regressive coefficient as a edge network, and evaluated the alpha centrality of each nodes

Human gut

Soil

Get the preprint